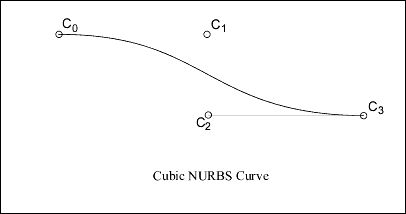
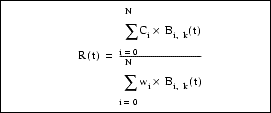Surface Parameterization
A surface in Creo contains data that describes the boundary of the surface, and a pointer to the primitive surface on which it lies. The primitive
surface is a three-dimensional geometric surface parameterized by two variables (u and v). The surface boundary consists of closed loops (contours) of edges. Each edge is attached to two surfaces, and each edge
contains the u and v values of the portion of the boundary that it forms for both surfaces. Surface boundaries are traversed clockwise around
the outside of a surface, so an edge has a direction in each surface with respect to the direction of traversal.
This section describes the surface parameterization. The surfaces are listed in order of complexity. For ease of use, the
alphabetical listing of the data structures is as follows:
Plane
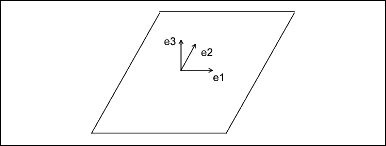
The plane entity consists of two perpendicular unit vectors (e1 and e2), the normal to the plane (e3), and the origin of the plane.
Data Format:
e1[3] Unit vector, in the u direction
e2[3] Unit vector, in the v direction
e3[3] Normal to the plane
origin[3] Origin of the plane
Parameterization:
(x, y, z) = u * e1 + v * e2 + originCylinder
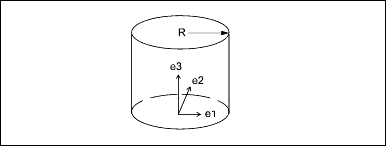
The generating curve of a cylinder is a line, parallel to the axis, at a distance R from the axis. The radial distance of a point is constant, and the height of the point is v.
Data Format:
e1[3] Unit vector, in the u direction
e2[3] Unit vector, in the v direction
e3[3] Normal to the plane
origin[3] Origin of the cylinder
radius Radius of the cylinder
Parameterization:
(x, y, z) = radius * [cos(u) * e1 + sin(u) * e2] +
v * e3 + originEngineering Notes:
For the cylinder, cone, torus, and general surface of revolution, a local coordinate system is used that consists of three
orthogonal unit vectors (e1, e2, and e3) and an origin. The curve lies in the plane of e1 and e3, and is rotated in the direction from e1 to e2. The u surface parameter determines the angle of rotation, and the v parameter determines the position of the point on the generating curve.
Cone
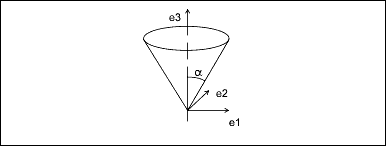
The generating curve of a cone is a line at an angle alpha to the axis of revolution that intersects the axis at the origin.
The v parameter is the height of the point along the axis, and the radial distance of the point is v * tan(alpha).
Data Format:
e1[3] Unit vector, in the u direction
e2[3] Unit vector, in the v direction
e3[3] Normal to the plane
origin[3] Origin of the cone
alpha Angle between the axis of the cone
and the generating lineParameterization:
(x, y, z) = v * tan(alpha) * [cos(u) * e1 +
sin(u) * e2] + v * e3 + originTorus
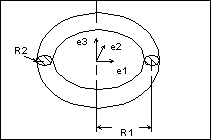
The generating curve of a torus is an arc of radius R2 with its center at a distance R1 from the origin. The starting point of the generating arc is located at a distance R1 + R2 from the origin, in the direction of the first vector of the local coordinate system. The radial distance of a point on the
torus is R1 + R2 * cos(v), and the height of the point along the axis of revolution is R2 * sin(v).
Data Format:
e1[3] Unit vector, in the u direction
e2[3] Unit vector, in the v direction
e3[3] Normal to the plane
origin[3] Origin of the torus
radius1 Distance from the center of the
generating arc to the axis of
revolution
radius2 Radius of the generating arc
Parameterization:
(x, y, z) = (R1 + R2 * cos(v)) * [cos(u) * e1 +
sin(u) * e2] + R2 * sin(v) * e3 +
originGeneral Surface of Revolution
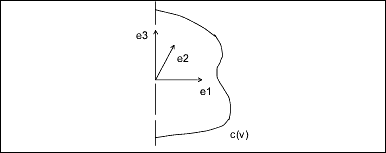
A general surface of revolution is created by rotating a curve entity, usually a spline, around an axis. The curve is evaluated
at the normalized parameter v, and the resulting point is rotated around the axis through an angle u. The surface of revolution data structure consists of a local coordinate system and a curve structure.
Data Format:
e1[3] Unit vector, in the u direction
e2[3] Unit vector, in the v direction
e3[3] Normal to the plane
origin[3] Origin of the surface of revolution
curve Generating curveParameterization:
curve(v) = (c1, c2, c3) is a point on the curve.
(x, y, z) = [c1 * cos(u) - c2 * sin(u)] * e1 +
[c1 * sin(u) + c2 * cos(u)] * e2 +
c3 * e3 + originRuled Surface
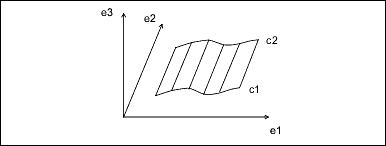
A ruled surface is the surface generated by interpolating linearly between corresponding points of two curve entities. The
u coordinate is the normalized parameter at which both curves are evaluated, and the v coordinate is the linear parameter between the two points. The curves are not defined in the local coordinate system of the
part, so the resulting point must be transformed by the local coordinate system of the surface.
Data Format:
e1[3] Unit vector, in the u direction
e2[3] Unit vector, in the v direction
e3[3] Normal to the plane
origin[3] Origin of the ruled surface
curve_1 First generating curve
curve_2 Second generating curveParameterization:
(x', y', z') is the point in local coordinates.
(x', y', z') = (1 - v) * C1(u) + v * C2(u)
(x, y, z) = x' * e1 + y' * e2 + z' * e3 + originTabulated Cylinder
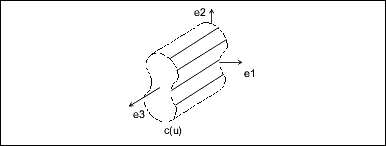
A tabulated cylinder is calculated by projecting a curve linearly through space. The curve is evaluated at the u parameter, and the z coordinate is offset by the v parameter. The resulting point is expressed in local coordinates and must be transformed by the local coordinate system to
be expressed in part coordinates.
Data Format:
e1[3] Unit vector, in the u direction
e2[3] Unit vector, in the v direction
e3[3] Normal to the plane
origin[3] Origin of the tabulated cylinder
curve Generating curveParameterization:
(x', y', z') is the point in local coordinates.
(x', y', z') = C(u) + (0, 0, v)
(x, y, z) = x' * e1 + y' * e2 + z' * e3 + originCoons Patch
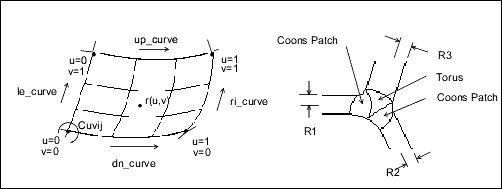
A Coons patch is used to blend surfaces together. For example, you would use a Coons patch at a corner where three fillets
(each of a different radius) meet.
Data Format:
le_curve u = 0 boundary
ri_curve u = 1 boundary
dn_curve v = 0 boundary
up_curve v = 1 boundary
point_matrix[2][2] Corner points
uvder_matrix[2][2] Corner mixed derivativesFillet Surface
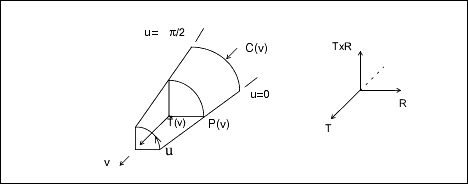
A fillet surface is found where a round or a fillet is placed on a curved edge, or on an edge with non-constant arc radii.
On a straight edge, a cylinder would be used to represent the fillet.
Data Format:
pnt_spline P(v) spline running along the u = 0 boundary
ctr_spline C(v) spline along the centers of the
fillet arcs
tan_spline T(v) spline of unit tangents to the
axis of the fillet arcsParameterization:
R(v) = P(v) - C(v)
(x,y,z) = C(v) + R(v) * cos(u) + T(v) X R(v) *
sin(u)Spline Surface
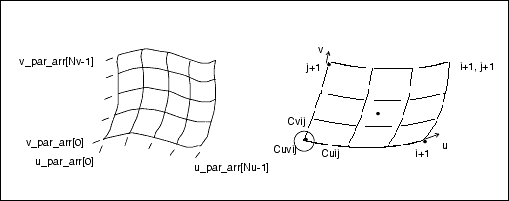
The parametric spline surface is a nonuniform bicubic spline surface that passes through a grid with tangent vectors given
at each point. The grid is curvilinear in uv space. Use this for bicubic blending between corner points.
Data Format:
u_par_arr[] Point parameters, in the u
direction, of size Nu
v_par_arr[] Point parameters, in the v
direction, of size Nv
point_arr[][3] Array of interpolant points, of
size Nu x Nv
u_tan_arr[][3] Array of u tangent vectors
at interpolant points, of size
Nu x Nv
v_tan_arr[][3] Array of v tangent vectors at
interpolant points, of size
Nu x Nv
uvder_arr[][3] Array of mixed derivatives at
interpolant points, of size
Nu x NvEngineering Notes:
| • | Allows for a unique 3x3 polynomial around every patch. |
| • | There is second order continuity across patch boundaries. |
| • | The point and tangent vectors represent the ordering of an array of [i][j], where u varies with j, and v varies with j. In walking through the point_arr[][3], you will find that the innermost variable representing v(j) varies first. |
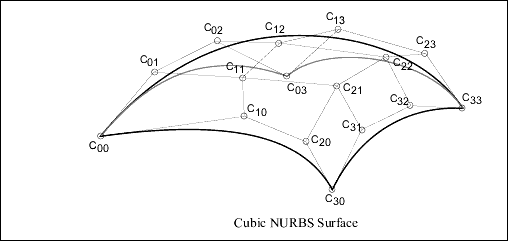
NURBS Surface
The NURBS surface is defined by basis functions (in u and v), expandable arrays of knots, weights, and control points.
Data Format:
deg[2] Degree of the basis
functions (in u and v)
u_par_arr[] Array of knots on the
parameter line u
v_par_arr[] Array of knots on the
parameter line v
wghts[] Array of weights for
rational NURBS, otherwise
NULL
c_point_arr[][3] Array of control pointsDefinition:
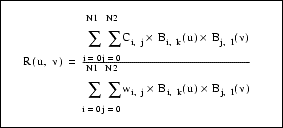
k = degree in u
l = degree in v
N1 = (number of knots in u) - (degree in u) - 2
N2 = (number of knots in v) - (degree in v) - 2
Bi,k = basis function in u
Bj, l = basis function in v
wij = weights
Ci, j = control points (x,y,z) * wi,jEngineering Notes:
The weights and c_points_arr arrays represent matrices of size wghts[N1+1] [N2+1] and c_points_arr [N1+1] [N2+1]. Elements of the matrices are packed into arrays in row-major order.
Cylindrical Spline Surface
The cylindrical spline surface is a nonuniform bicubic spline surface that passes through a grid with tangent vectors given
at each point. The grid is curvilinear in modeling space.
Data Format:
e1[3] x' vector of the local coordinate
system
e2[3] y' vector of the local coordinate
system
e3[3] z' vector of the local coordinate
system, which corresponds to the
axis of revolution of the surface
origin[3] Origin of the local coordinate
system
splsrf Spline surface data structureThe spline surface data structure contains the following fields:
u_par_arr[] Point parameters, in the
u direction, of size Nu
v_par_arr[] Point parameters, in the
v direction, of size Nv
point_arr[][3] Array of points, in
cylindrical coordinates,
of size Nu x Nv. The array
components are as follows:
point_arr[i][0] - Radius
point_arr[i][1] - Theta
point_arr[i][2] - Z
u_tan_arr[][3] Array of u tangent vectors.
in cylindrical coordinates,
of size Nu x Nv
v_tan_arr[][3] Array of v tangent vectors,
in cylindrical coordinates,
of size Nu x Nv
uvder_arr[][3] Array of mixed derivatives,
in cylindrical coordinates,
of size Nu x NvEngineering Notes:
If the surface is represented in cylindrical coordinates (r, theta, z), the local coordinate system values (x',y', z') are interpreted as follows:
x' = r cos (theta)
y' = r sin (theta)
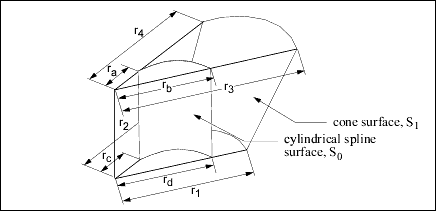
z' = zA cylindrical spline surface can be obtained, for example, by creating a smooth rotational blend (shown in the figure).
In some cases, you can replace a cylindrical spline surface with a surface such as a plane, cylinder, or cone. For example,
in the figure, the cylindrical spline surface S1 was replaced with a cone (r1 = r2, r3 = r4, and r1 ≠ r3).
If a replacement cannot be done (such as for the surface S0 in the figure (ra ≠ rb or rc ≠ rd)), leave it as a cylindrical spline surface representation.